I am a PIMS-Simons Postdoctoral Fellow working with the group of Christoph Ortner at the University of British Columbia. Previously I held a postdoctoral research associate position at the University of Oxford after having completed a PhD in applied mathematics at the Imperial College London.
My research focus is the development of computational tools for PDEs, integral equations and fractional differential equations with applications in the natural sciences such as quantum physics and collective behavior in biology, including specifically also machine learning models thereof. I am also more generally interested in computational orthogonal polynomials and their applications in such methods.
The following is a non-exhaustive list of things I have worked on and am currently interested in.
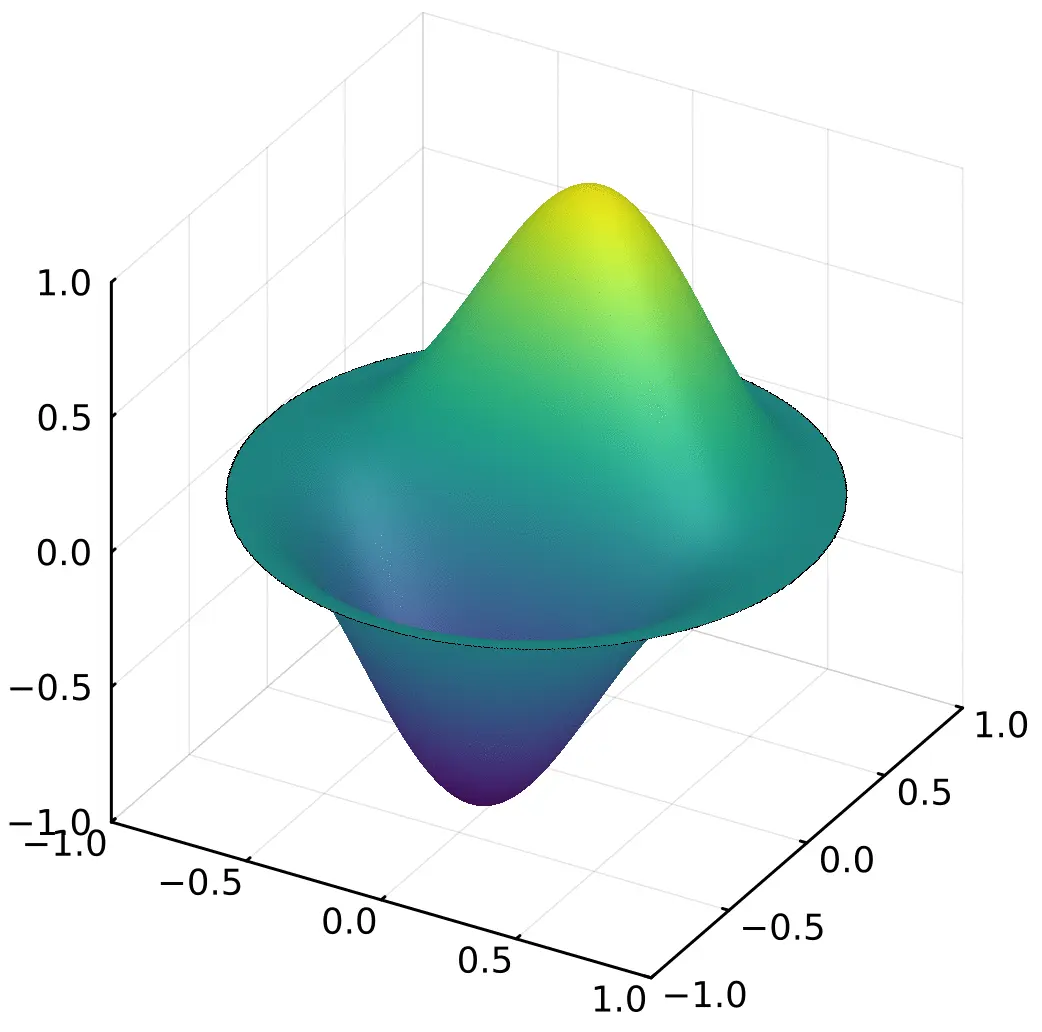
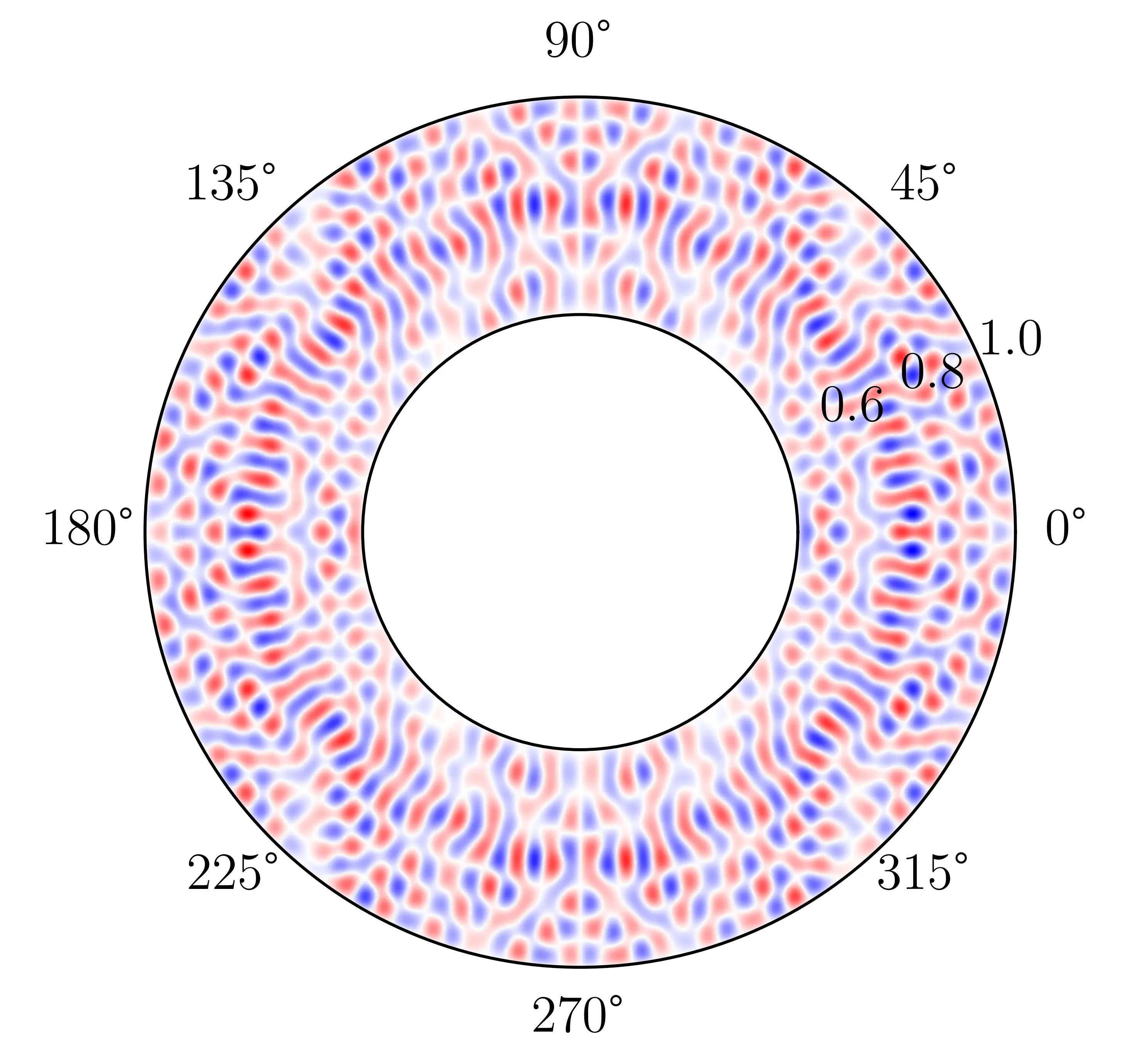
Conical intersections play a crucial role in determining the dynamics of molecules and materials upon light excitation, molecular orbitals and material band structure. In the relevant context of high-dimensional non-smooth hyper-surfaces, common machine learning models perform poorly.
I have worked on overcoming these issues by learning globally smooth invariant quantities from which the desired conical intersections can be reconstructed accurately.
Many physical and biological systems can be accurately modeled using atomistic many body interactions. Machine learning based methods allow one to infer succesful models for otherwise prohibitively large and complex systems.
I work on novel methodologies and applications of such frameworks as well as the closely related problem of analyzing their theoretical foundations.
Fractional differential equations generalize ODEs and PDEs to include derivative operators of non-integer order. The resulting operators are generally nonlocal and thus pose several challenges to conventional numerical approaches.
Fractional derivatives and closely related objects such as Riesz potentials appear in applications featuring memory effects, e.g. photoacoustic imaging in medical physics or in the continuous limit of classical particle swarms.
Orthogonal polynomials can be used to accurately and efficiently approximate functions.
With appropriate orthogonal polynomials for a given domain and weight function in hand one can construct quadrature methods as well as spectral methods for solving integral and partial differential equations with sparse discretisations and spectral convergence.
See also the automated listings at Google Scholar or Semantic Scholar.
Below is a selection of my conference talks. I'll update the website with a more complete list soon.